Note
Go to the end to download the full example code.
Using Coala within Shamrock to solve the Smoluchowski equation#
Imports
9 import os
10
11 import numpy as np
12 import shamrock.external.coala as coala
13 from matplotlib import pyplot as plt
Where is coala located?
17 print(f"coala path : {coala.__file__}")
coala path : /__w/Shamrock/Shamrock/.pyvenv/lib/python3.12/site-packages/shamrock/external/coala/__init__.py
Parameters of the dust distribution & evolution
22 nbins = 20
23
24 massmax = 1e6
25 massmin = 1e-3
26
27 kernel = 1
28 K0 = 1.0
29 Q = 5
30 eps = 1e-20
31 coeff_CFL = 0.3
32 t0 = 0.0
33
34 cases = {
35 "order k=0": {
36 "kpol": 0,
37 },
38 "order k=1": {
39 "kpol": 1,
40 },
41 "order k=2": {
42 "kpol": 2,
43 },
44 }
45
46 if kernel == 0:
47 dthydro = 100
48 ndthydro = 300
49 elif kernel == 1:
50 dthydro = 1e-2
51 ndthydro = 300
52 elif kernel == 2:
53 dthydro = 1e-1
54 ndthydro = 500
55 elif kernel == 3:
56 dthydro = 1e-1
57 ndthydro = 500
58 else:
59 raise ValueError("need to choose a kernel")
60
61 massgrid, massbins = coala.init_grid_log(nbins, massmax, massmin)
62
63 for case in cases:
64 kpol = cases[case]["kpol"]
65 match kernel:
66 case 0 | 1 | 2:
67 gij_init, gij, time_coag = coala.iterate_coag(
68 kernel, K0, nbins, kpol, dthydro, ndthydro, coeff_CFL, Q, eps, massgrid, massbins
69 )
70
71 case 3:
72 # Brownian motion dv with constant approximation
73 dv_Br = np.zeros((nbins, nbins))
74 massmeanlog = np.sqrt(massgrid[0:nbins] * massgrid[1:])
75 for i in range(nbins):
76 for j in range(nbins):
77 dv_Br[i, j] = np.sqrt(1.0 / massmeanlog[i] + 1.0 / massmeanlog[j])
78
79 gij_init, gij, time_coag = coala.iterate_coag_kdv(
80 kernel,
81 K0,
82 nbins,
83 kpol,
84 dthydro,
85 ndthydro,
86 coeff_CFL,
87 Q,
88 eps,
89 massgrid,
90 massbins,
91 dv_Br,
92 )
93
94 case _:
95 print("Need to choose available kernel in kernel_collision.py.")
96
97 cases[case]["massgrid"] = massgrid
98 cases[case]["massbins"] = massbins
99 cases[case]["gij_init"] = gij_init
100 cases[case]["gij_end"] = gij
101 cases[case]["time"] = [t0, time_coag]
Tensor tabflux generated in 0.25580 s
gij generated in 0.00018 s
gij t0 = [1.90527518e-03 5.34978592e-03 1.49200031e-02 4.08236317e-02
1.05876532e-01 2.36603895e-01 3.53238069e-01 1.92536780e-01
1.28210758e-02 7.88742300e-06 5.05922357e-15 1.00000000e-20
1.00000000e-20 1.00000000e-20 1.00000000e-20 1.00000000e-20
1.00000000e-20 1.00000000e-20 1.00000000e-20 1.00000000e-20]
M1 t0 = 0.9999988304202374
Time solver in progress
total nsub = 300
total ndt = 227
total number time-steps = 527
gij tend = [9.46923595e-05 2.65043632e-04 7.32678756e-04 1.95693839e-03
4.76890398e-03 9.28871278e-03 1.15251017e-02 7.84524840e-03
4.18790882e-03 2.15758465e-03 1.11809027e-03 5.73274221e-04
2.79582274e-04 1.24810694e-04 4.80539799e-05 1.45278618e-05
3.02547109e-06 3.71308293e-07 2.26007997e-08 5.67256497e-10]
M1 t0 = 0.9999988304202374
M1 tend = 0.9999988304202367
diff M1 = -6.661338147750939e-16
Time solver in 0.05474
Tensor tabflux tabintflux generated in 8.23964 s
gij generated in 0.00072 s
gij t0 = [[ 1.90527518e-03 9.05725016e-04]
[ 5.34978592e-03 2.53498952e-03]
[ 1.49200031e-02 7.00550421e-03]
[ 4.08236317e-02 1.86714390e-02]
[ 1.05876532e-01 4.47777100e-02]
[ 2.36603895e-01 7.68481264e-02]
[ 3.53238069e-01 1.50847901e-02]
[ 1.92536780e-01 -1.40538593e-01]
[ 1.28210758e-02 -1.28210758e-02]
[ 7.88742300e-06 -7.88742300e-06]
[ 5.05922357e-15 -5.05921357e-15]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00]]
M1 t0 = 0.9999988304202374
Time solver in progress
total nsub = 201
total ndt = 254
total number time-steps = 455
gij tend = [[ 9.46748867e-05 4.49313443e-05]
[ 2.64905195e-04 1.24935394e-04]
[ 7.31591213e-04 3.38957363e-04]
[ 1.94859122e-03 8.57842302e-04]
[ 4.70971706e-03 1.78004402e-03]
[ 8.97837560e-03 2.02344363e-03]
[ 1.09628859e-02 -3.93487186e-04]
[ 8.44513302e-03 -1.48433949e-03]
[ 5.14873253e-03 -1.06071864e-03]
[ 3.03683434e-03 -6.13512395e-04]
[ 1.77279721e-03 -3.39368817e-04]
[ 1.00204189e-03 -2.09442170e-04]
[ 5.04192232e-04 -1.41730972e-04]
[ 1.86341177e-04 -8.79482101e-05]
[ 3.25424160e-05 -2.82716732e-05]
[ 1.23991390e-06 -1.23991390e-06]
[ 1.01484523e-08 -1.01484523e-08]
[ 2.08646952e-11 -2.08646952e-11]
[ 6.75735584e-15 -6.75734584e-15]
[ 3.27695741e-19 -3.17695741e-19]]
M1 t0 = 0.9999988304202374
M1 tend = 0.9999988304202367
diff M1 = -6.661338147750939e-16
Time solver in 0.68107
Tensor tabflux tabintflux generated in 36.21424 s
gij generated in 0.00497 s
gij t0 = [[ 1.90527518e-03 9.05725016e-04 -5.49509960e-07]
[ 5.34978592e-03 2.53498952e-03 -4.34223153e-06]
[ 1.49200031e-02 7.00550421e-03 -3.39884114e-05]
[ 4.08236317e-02 1.86714390e-02 -2.59000879e-04]
[ 1.05876532e-01 4.47777100e-02 -1.82867015e-03]
[ 2.36603895e-01 7.68481264e-02 -1.03458457e-02]
[ 3.53238069e-01 1.50847901e-02 -2.89427354e-02]
[ 1.92536780e-01 -1.40538593e-01 1.94501341e-02]
[ 1.28210758e-02 -2.10736118e-02 1.68642939e-02]
[ 7.88742300e-06 -1.01855598e-05 1.31438063e-05]
[ 5.05922357e-15 -6.34995441e-15 8.54561595e-15]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]
[ 1.00000000e-20 0.00000000e+00 0.00000000e+00]]
M1 t0 = 0.9999988304202374
Time solver in progress
total nsub = 197
total ndt = 271
total number time-steps = 468
gij tend = [[ 9.46740930e-05 4.49306564e-05 -5.30725953e-08]
[ 2.64898939e-04 1.24930186e-04 -4.16260358e-07]
[ 7.31542559e-04 3.38921500e-04 -3.19048882e-06]
[ 1.94822620e-03 8.57669602e-04 -2.29199278e-05]
[ 4.70720297e-03 1.78056407e-03 -1.37297806e-04]
[ 8.96373187e-03 2.04516882e-03 -4.95078148e-04]
[ 1.09001508e-02 -2.95227344e-04 -3.90237343e-04]
[ 8.36656837e-03 -1.65208521e-03 2.89923760e-04]
[ 5.25686775e-03 -1.25407691e-03 2.62553011e-04]
[ 3.16148600e-03 -7.64386129e-04 1.75976220e-04]
[ 1.87293760e-03 -4.28005126e-04 8.32321583e-05]
[ 1.06532175e-03 -2.58924824e-04 3.24894494e-05]
[ 5.33049416e-04 -1.78936288e-04 1.85477876e-05]
[ 1.85170566e-04 -1.14608901e-04 1.94401344e-05]
[ 2.57319638e-05 -3.31284417e-05 1.23865040e-05]
[ 6.36584472e-07 -1.08681430e-06 7.43906502e-07]
[ 1.38512136e-08 -2.12361893e-08 2.02956586e-08]
[ 2.95845862e-10 -3.62377036e-10 5.05016610e-10]
[ 9.06693425e-13 -1.01043556e-12 1.60078727e-12]
[ 1.91516589e-16 -2.08222215e-16 3.40579088e-16]]
M1 t0 = 0.9999988304202374
M1 tend = 0.9999988304202387
diff M1 = 1.3322676295501878e-15
Time solver in 5.29726
Plotting
106 plt.rcParams["font.size"] = 16
107 plt.rcParams["lines.linewidth"] = 3
108 plt.rcParams["legend.columnspacing"] = 0.5
109
110 savefig_options = dict(bbox_inches="tight")
111
112 marker_style = dict(
113 marker="o", markersize=8, markerfacecolor="white", linestyle="", markeredgewidth=2
114 )
115
116 match kernel:
117 case 0:
118 str_kernel = "kconst"
119 case 1:
120 str_kernel = "kadd"
121 case _:
122 print("Need to choose a simple kernel in the list.")
123
124
125 x = np.logspace(np.log10(massmin), np.log10(massmax), num=100)
126
127 tend = cases["order k=0"]["time"][-1]
128 plt.figure(1)
129 plt.loglog(x, coala.exact_sol_coag(kernel, x, 0.0), "--", c="C0", alpha=0.5)
130 plt.loglog(x, coala.exact_sol_coag(kernel, x, tend), "--", c="C0", label="Analytic")
131
132 plt.loglog(
133 cases["order k=0"]["massbins"],
134 cases["order k=0"]["gij_init"],
135 markeredgecolor="black",
136 label="gij init",
137 **marker_style,
138 alpha=0.5,
139 )
140 for case in cases:
141 print("plotting case", case)
142
143 # if cases[case]["gij_end"][0] is a scalar
144 print("gij_end = ", type(cases[case]["gij_end"][0]))
145 if isinstance(cases[case]["gij_end"][0], np.float64):
146 print("gij_end is a scalar")
147 plt.loglog(cases[case]["massbins"], cases[case]["gij_end"], label=case, **marker_style)
148 else:
149 print("gij_end is an array")
150 plt.loglog(
151 cases[case]["massbins"], cases[case]["gij_end"][:, 0], label=case, **marker_style
152 )
153 # print ("gij_end = ",type(cases[case]["gij_end"][0]))
154 # plt.loglog(cases[case]["massbins"],cases[case]["gij_end"],markeredgecolor='black',label=case,**marker_style)
155
156 plt.ylim(1.0e-15, 1.0e1)
157 plt.xlim(massmin, massmax)
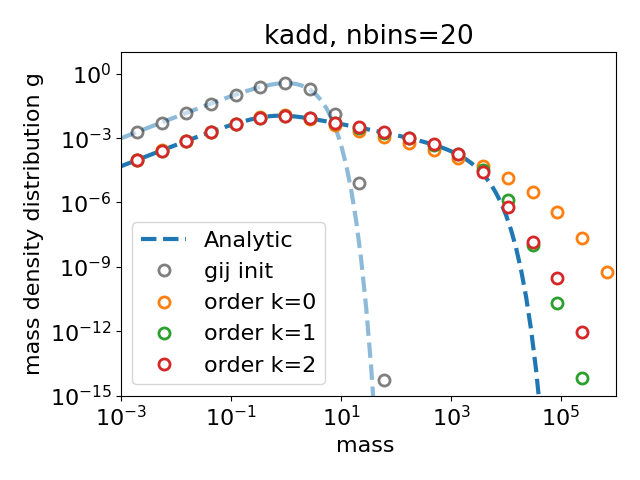
158 plt.title(str_kernel + ", nbins=%d" % (nbins))
159 plt.xlabel(r"mass ")
160 plt.ylabel(r"mass density distribution g")
161 plt.legend(loc="lower left", ncol=1)
162 plt.tight_layout()
163
164 plt.show()
plotting case order k=0
gij_end = <class 'numpy.float64'>
gij_end is a scalar
plotting case order k=1
gij_end = <class 'numpy.ndarray'>
gij_end is an array
plotting case order k=2
gij_end = <class 'numpy.ndarray'>
gij_end is an array
Total running time of the script: (0 minutes 51.466 seconds)
Estimated memory usage: 160 MB
