Note
Go to the end to download the full example code.
Paving functions#
This simple example shows how paving functions in Shamrock works
9 import matplotlib.pyplot as plt
10 import numpy as np
11
12 import shamrock
Use shamrock documentation style for matplotlib
17 shamrock.matplotlib.set_shamrock_mpl_style()
Set box size
23 box_size_x = 2.0
24 box_size_y = 2.0
Particle set
29 parts = [
30 {"x": 0.1 * box_size_x, "y": 0.1 * box_size_y, "color": "blue"},
31 {"x": 0.7 * box_size_x, "y": 0.1 * box_size_y, "color": "red"},
32 {"x": 0.1 * box_size_x, "y": 0.7 * box_size_y, "color": "green"},
33 {"x": 0.7 * box_size_x, "y": 0.7 * box_size_y, "color": "black"},
34 ]
Utility to plot the paving function
41 def add_rect(x, y, w, h):
42 plt.gca().add_patch(
43 plt.Rectangle((x, y), w, h, alpha=0.5, fill=True, facecolor="grey", linewidth=2)
44 )
45
46
47 def plot_paving_function(pav_func, pav_func_name, shear_x=0.0):
48 plt.figure()
49 for i in range(-2, 3):
50 for j in range(-3, 4):
51 # j = i
52 add_rect(
53 0.05 + i * box_size_x + shear_x * j,
54 0.05 + j * box_size_y,
55 box_size_x - 0.1,
56 box_size_y - 0.1,
57 )
58
59 for part in parts:
60 x, y, z = pav_func.f((part["x"], part["y"], 0.0), i, j, 0)
61
62 plt.scatter(x, y, color=part["color"])
63 plt.title(f"Paving function: {pav_func_name}")
64 plt.xlabel("x")
65 plt.ylabel("y")
66
67 plt.figure()
68 for i in range(-2, 3):
69 for j in range(-3, 4):
70 add_rect(
71 0.05 + i * box_size_x + shear_x * j,
72 0.05 + j * box_size_y,
73 box_size_x - 0.1,
74 box_size_y - 0.1,
75 )
76
77 for part in parts:
78 x, y, z = pav_func.f((part["x"], part["y"], 0.0), i, j, 0)
79
80 x_2, y_2, z_2 = pav_func.f_inv((x, y, 0.0), i, j, 0)
81
82 delta_x = x_2 - part["x"]
83 delta_y = y_2 - part["y"]
84
85 if abs(delta_x) > 1e-4 or abs(delta_y) > 1e-4:
86 print("error")
87
88 plt.scatter(x_2 + 0.1 * i, y_2 + 0.1 * j, color=part["color"])
89 plt.title(f"Paving function inverse: {pav_func_name}")
90 plt.xlabel("x")
91 plt.ylabel("y")
Testing the paving functions#
Periodic paving function
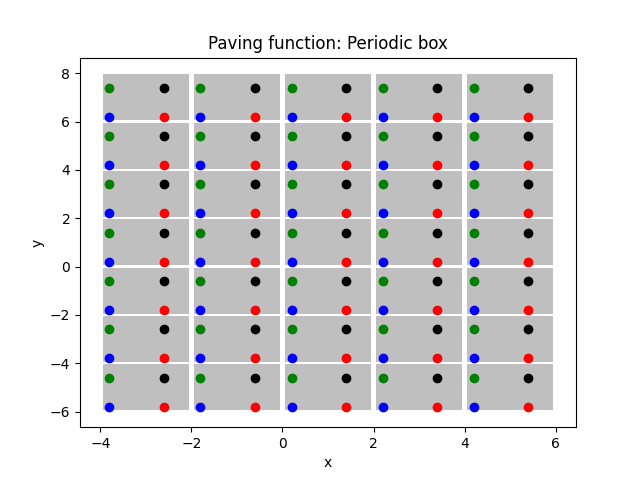
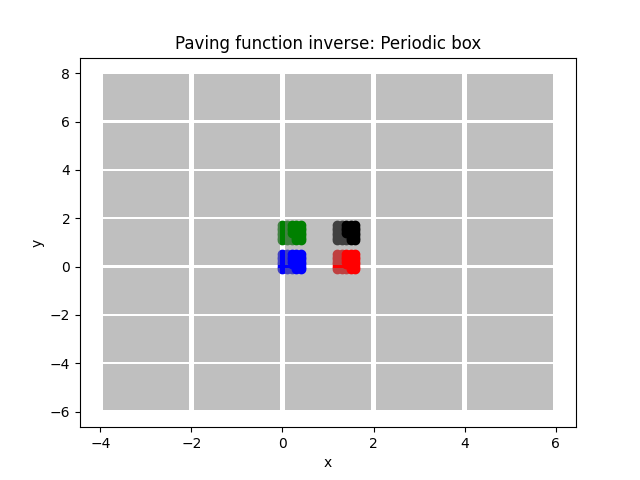
101 plot_paving_function(
102 shamrock.math.paving_function_general_3d(
103 (box_size_x, box_size_y, 0.0), (box_size_x / 2.0, box_size_y / 2.0, 0.0), True, True, True
104 ),
105 "Periodic box",
106 )
Periodic & reflective paving function
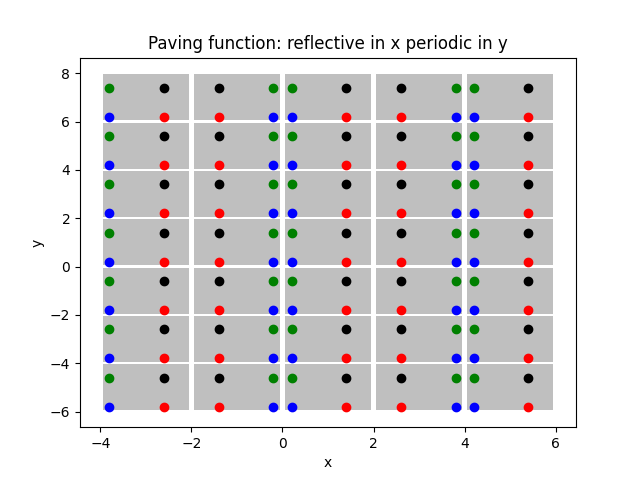
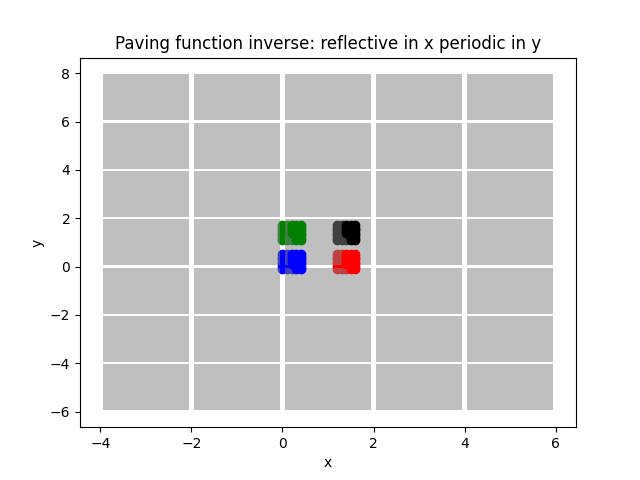
112 plot_paving_function(
113 shamrock.math.paving_function_general_3d(
114 (box_size_x, box_size_y, 0.0), (box_size_x / 2.0, box_size_y / 2.0, 0.0), False, True, True
115 ),
116 "reflective in x periodic in y",
117 )
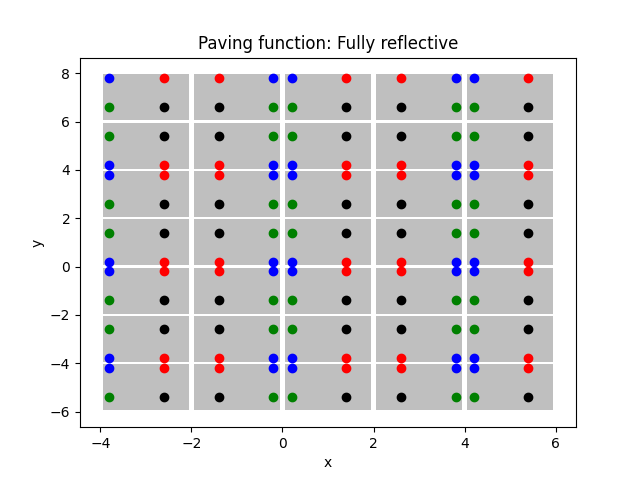
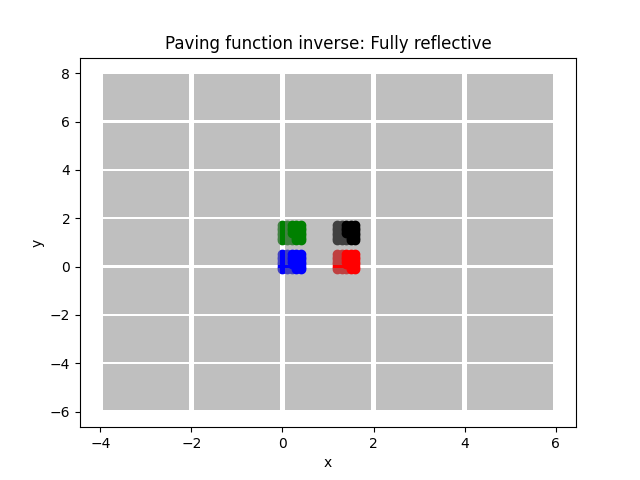
Fully reflective paving function
123 plot_paving_function(
124 shamrock.math.paving_function_general_3d(
125 (box_size_x, box_size_y, 0.0), (box_size_x / 2.0, box_size_y / 2.0, 0.0), False, False, True
126 ),
127 "Fully reflective",
128 )
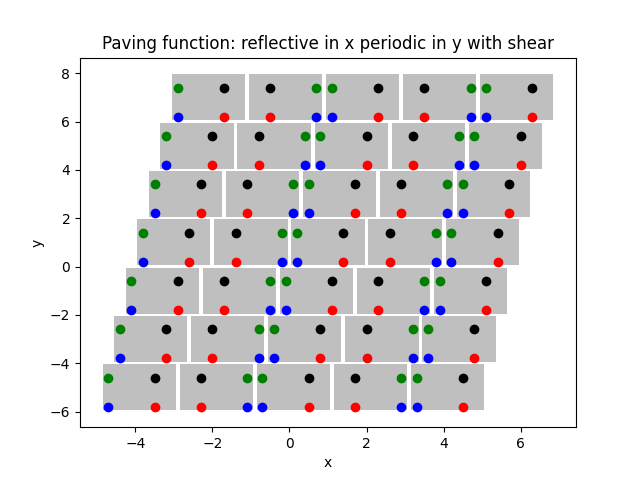
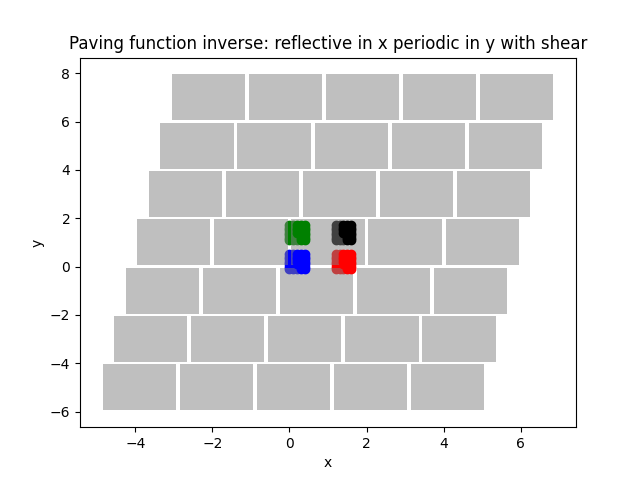
Periodic & reflective paving function with shear
134 plot_paving_function(
135 shamrock.math.paving_function_general_3d_shear_x(
136 (box_size_x, box_size_y, 0.0),
137 (box_size_x / 2.0, box_size_y / 2.0, 0.0),
138 False,
139 True,
140 True,
141 0.3,
142 ),
143 "reflective in x periodic in y with shear",
144 shear_x=0.3,
145 )
146
147 plt.show()
Total running time of the script: (0 minutes 4.682 seconds)
Estimated memory usage: 160 MB