Ghost layer generation using paving functions

This example showcase how to use the paving functions to generate ghost layers.

The complex thing is that we want to intersect the current data with the ghost layer, but we do not want to modify the original buffer. As a result we perform the intersection in a space transformed by the paving function, and then map the result back to the original space.

Formally speaking for a paving function f:

\[\text{Ghost layer} = f(\text{patch}) \vee \text{box} \ = f( f^{-1}(f(\text{patch}) \vee \text{box}) ) \ = f( \text{patch} \vee f^{-1}(\text{box}) ),\]

where \(\vee\) denotes a ghost layer intersection.

import matplotlib.pyplot as plt
import numpy as np

import shamrock

Set box size

box_size_x = 2.0
box_size_y = 2.0
box_size_z = 2.0

Particle set

color_set = [
    "blue",
    "red",
    "green",
    "black",
    "orange",
    "purple",
    "brown",
    "pink",
    "gray",
    "olive",
    "cyan",
    "magenta",
    "yellow",
    "teal",
    "navy",
    "gold",
    "lime",
    "indigo",
    "maroon",
    "turquoise",
]

x_set = np.linspace(0.2, box_size_x - 0.2, 4)
y_set = np.linspace(0.2, box_size_y - 0.2, 4)

parts = []
i = 0
for x in x_set:
    for y in y_set:
        parts.append({"x": x, "y": y, "color": color_set[i % len(color_set)]})
        i += 1

Utility to plot the paving function

margin = 0.0


def add_rect(x, y, w, h, facecolor="grey", alpha=0.5):
    plt.gca().add_patch(
        plt.Rectangle(
            (x + margin, y + margin),
            w - 2 * margin,
            h - 2 * margin,
            alpha=alpha,
            fill=True,
            facecolor=facecolor,
            edgecolor="black",
            linewidth=4,
        )
    )


def add_rect_aabb(aabb, facecolor="grey", alpha=0.5):
    add_rect(
        aabb.lower[0],
        aabb.lower[1],
        aabb.upper[0] - aabb.lower[0],
        aabb.upper[1] - aabb.lower[1],
        facecolor=facecolor,
        alpha=alpha,
    )


def ghost_intersect(part, box_to_intersect):
    """
    dummy ghost layer intersection to showcase how it works
    """
    x, y, z = part["x"], part["y"], 0.0

    part_aabb = shamrock.math.AABB_f64_3((x - 0.3, y - 0.3, 0.0), (x + 0.3, y + 0.3, 0.0))

    intersect = box_to_intersect.get_intersect(part_aabb)

    _x, _y, _z = intersect.upper
    _z = 1.0  # we want to be sure that the volume is not null but the z is not used
    intersect.upper = (_x, _y, _z)

    return intersect.is_volume_not_null()


def plot_paving_function(pav_func, pav_func_name):
    box_to_intersect = shamrock.math.AABB_f64_3((0.0, 0.0, 0.0), (box_size_x, box_size_y, 0.0))

    def get_indices():
        for i in range(-3, 4):
            for j in range(-2, 3):
                if i == 0 and j == 0:
                    continue
                yield i, j

    plt.figure()

    for i, j in get_indices():
        box_to_intersect_inv_mapped = pav_func.f_aabb_inv(box_to_intersect, i, j, 0)

        add_rect_aabb(box_to_intersect_inv_mapped)

    for part in parts:
        x, y, z = (part["x"], part["y"], 0.0)
        plt.scatter(x, y, color=part["color"])

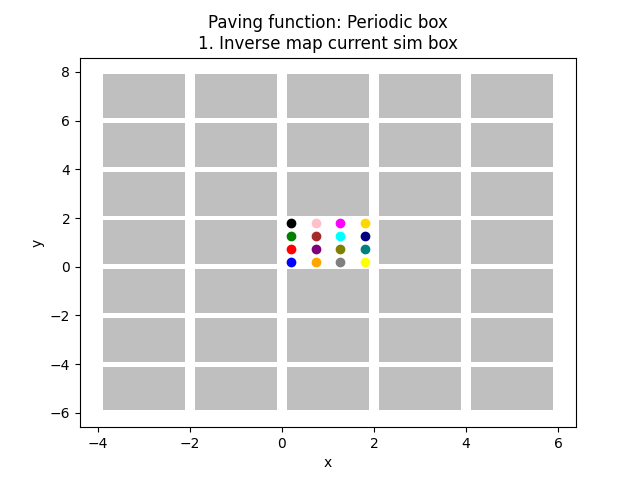
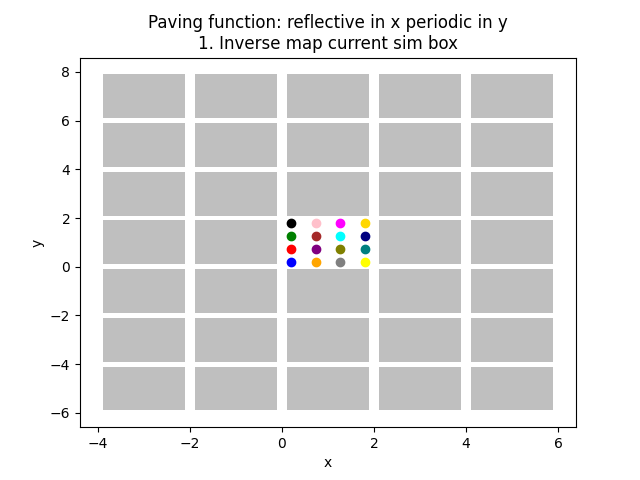
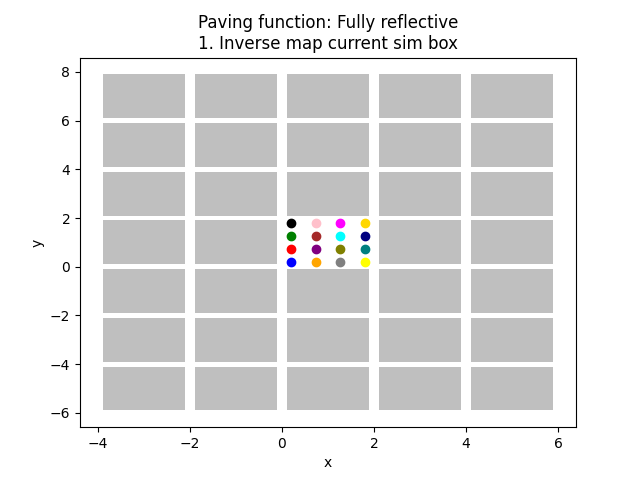
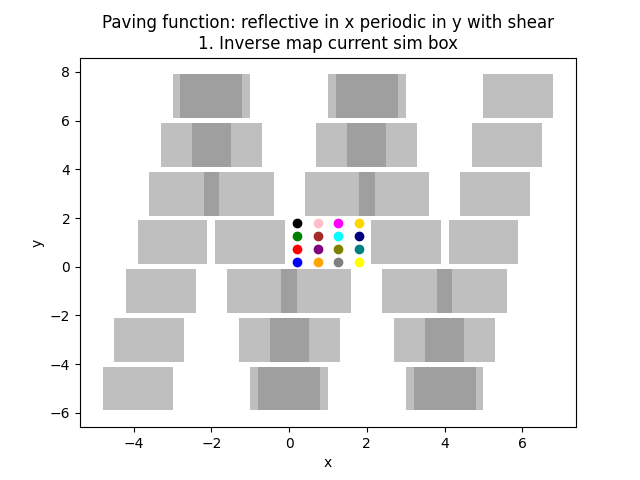
    plt.title(f"Paving function: {pav_func_name}\n1. Inverse map current sim box")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.axis("equal")

    plt.figure()

    for i, j in get_indices():
        box_to_intersect_inv_mapped = pav_func.f_aabb_inv(box_to_intersect, i, j, 0)

        add_rect_aabb(box_to_intersect_inv_mapped)

        for part in parts:
            x, y, z = (part["x"], part["y"], 0.0)
            if ghost_intersect(part, box_to_intersect_inv_mapped):
                plt.scatter(x, y, color=part["color"])

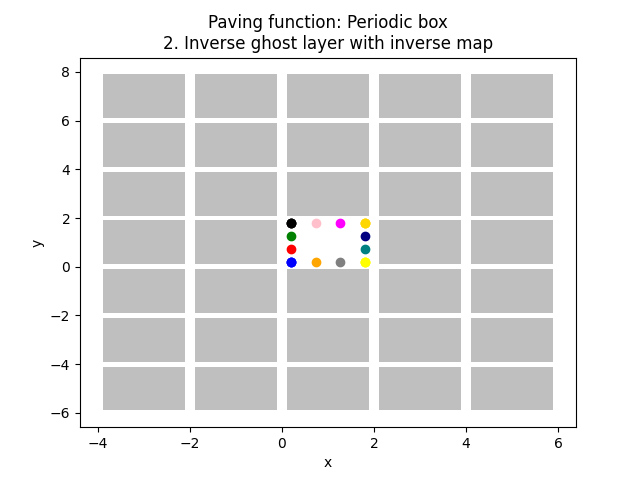
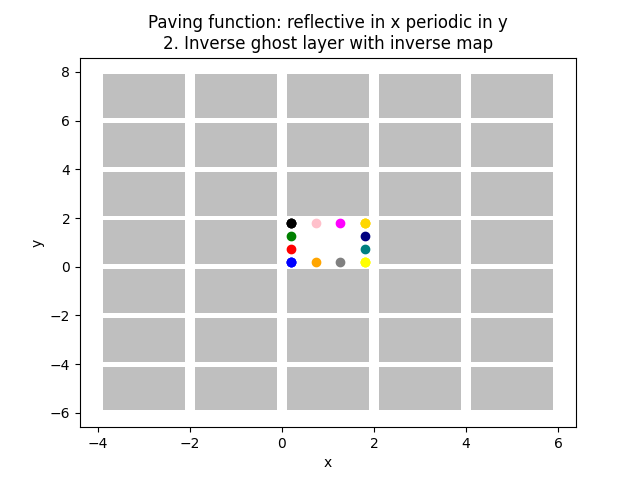
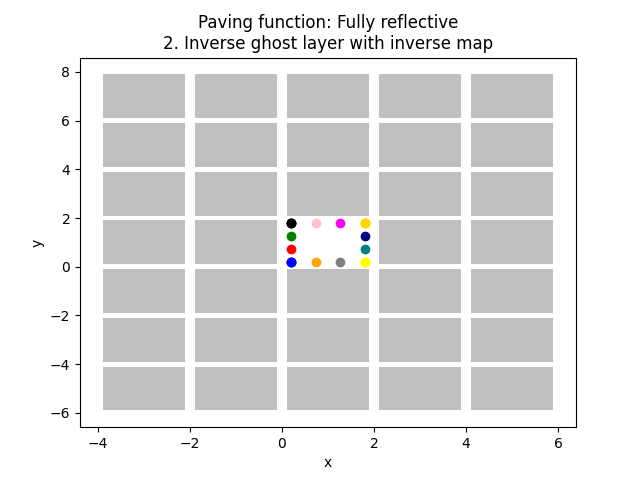
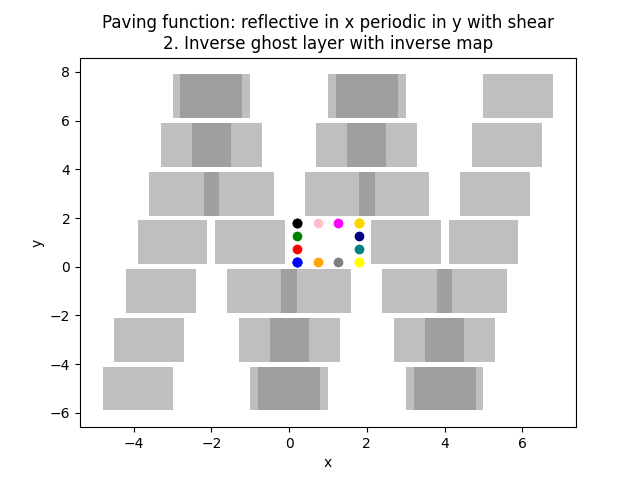
    plt.title(f"Paving function: {pav_func_name}\n2. Inverse ghost layer with inverse map")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.axis("equal")

    plt.figure()

    for i, j in get_indices():
        box_to_intersect_inv_mapped = pav_func.f_aabb_inv(box_to_intersect, i, j, 0)
        box_to_intersect_mapped = pav_func.f_aabb(box_to_intersect, i, j, 0)

        add_rect_aabb(box_to_intersect_mapped)

        for part in parts:
            x, y, z = (part["x"], part["y"], 0.0)

            if ghost_intersect(part, box_to_intersect_inv_mapped):
                x, y, z = pav_func.f((x, y, 0.0), i, j, 0)
                plt.scatter(x, y, color=part["color"])

    for part in parts:
        x, y, z = (part["x"], part["y"], 0.0)
        plt.scatter(x, y, color=part["color"])

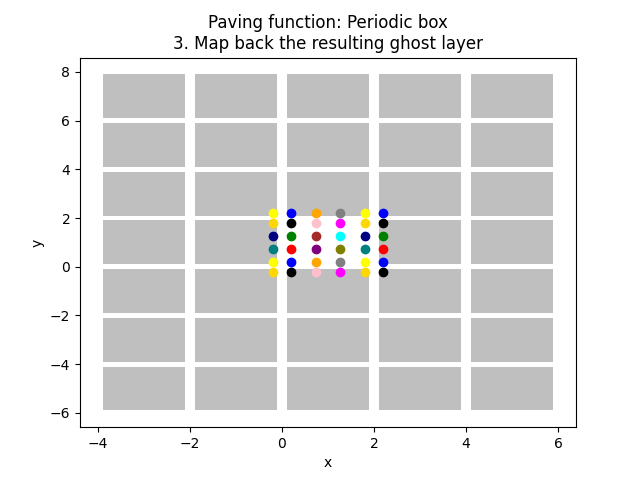
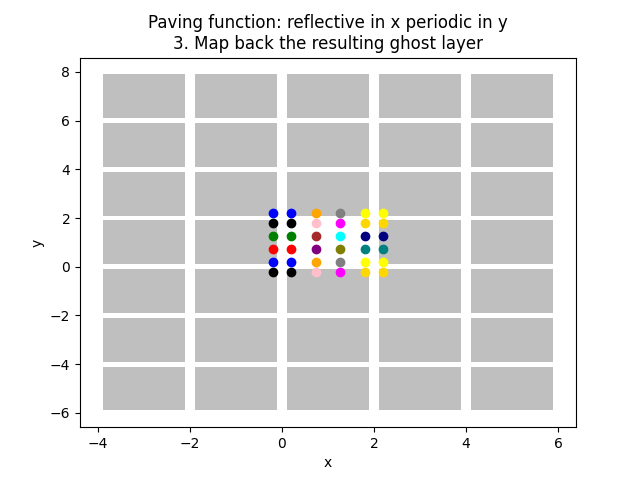
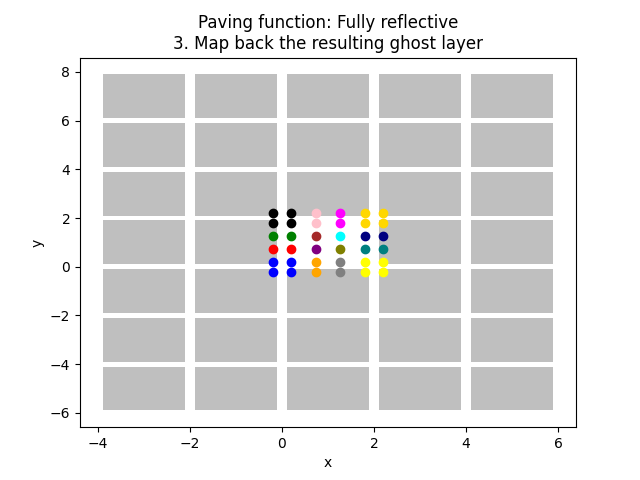
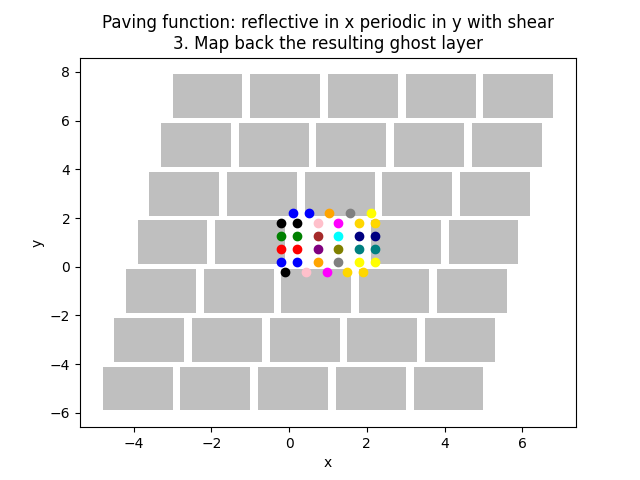
    plt.title(f"Paving function: {pav_func_name}\n3. Map back the resulting ghost layer")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.axis("equal")

Testing the paving functions

Periodic paving function

plot_paving_function(
    shamrock.math.paving_function_general_3d(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        True,
        True,
        True,
    ),
    "Periodic box",
)

• 
• 
• 

Periodic & reflective paving function

plot_paving_function(
    shamrock.math.paving_function_general_3d(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        True,
        True,
    ),
    "reflective in x periodic in y",
)

• 
• 
• 

Fully reflective paving function

plot_paving_function(
    shamrock.math.paving_function_general_3d(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        False,
        True,
    ),
    "Fully reflective",
)

• 
• 
• 

Periodic & reflective paving function with shear

plot_paving_function(
    shamrock.math.paving_function_general_3d_shear_x(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        True,
        True,
        0.3,
    ),
    "reflective in x periodic in y with shear",
)

• 
• 
• 

Testing the list of indices with the paving function

def test_paving_index_intersecting(pav_func, pav_func_name):
    radius_int = 3.5
    box_to_intersect = shamrock.math.AABB_f64_3(
        (box_size_x / 2 - radius_int, box_size_y / 2 - radius_int, box_size_z / 2 - radius_int),
        (box_size_x / 2 + radius_int, box_size_y / 2 + radius_int, box_size_z / 2 + radius_int),
    )

    indices = pav_func.get_paving_index_intersecting(box_to_intersect)

    def get_indices():
        x_r = 6
        y_r = 4
        for i in range(-x_r, x_r + 1):
            for j in range(-y_r, y_r + 1):
                yield i, j

    domain = shamrock.math.AABB_f64_3((0.0, 0.0, 0.0), (box_size_x, box_size_y, box_size_z))

    plt.figure()

    for i, j in get_indices():
        domain_mapped = pav_func.f_aabb(domain, i, j, 0)

        if [i, j, 0] in indices:
            add_rect_aabb(domain_mapped, facecolor="green")
        else:
            add_rect_aabb(domain_mapped, facecolor="grey")

    add_rect_aabb(box_to_intersect, facecolor="lightblue", alpha=0.5)

    plt.title(f"Paving function: {pav_func_name}\n")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.axis("equal")

Periodic paving function

test_paving_index_intersecting(
    shamrock.math.paving_function_general_3d(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        True,
        True,
        True,
    ),
    "Periodic box",
)

Periodic & reflective paving function

test_paving_index_intersecting(
    shamrock.math.paving_function_general_3d(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        True,
        True,
    ),
    "reflective in x periodic in y",
)

Fully reflective paving function

test_paving_index_intersecting(
    shamrock.math.paving_function_general_3d(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        False,
        True,
    ),
    "Fully reflective",
)

Periodic & reflective paving function with shear

test_paving_index_intersecting(
    shamrock.math.paving_function_general_3d_shear_x(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        True,
        True,
        0.3,
    ),
    "reflective in x periodic in y with shear",
)

Periodic & reflective paving function with strong shear

test_paving_index_intersecting(
    shamrock.math.paving_function_general_3d_shear_x(
        (box_size_x, box_size_y, box_size_z),
        (box_size_x / 2.0, box_size_y / 2.0, box_size_z / 2.0),
        False,
        True,
        True,
        1.8,
    ),
    "reflective in x periodic in y with shear",
)

plt.show()

Estimated memory usage: 159 MB